时间,节奏与动画编辑
本篇讨论了贝塞尔曲线的概念及其在动画中的应用,并通过JavaScript示例演示了如何计算和绘制贝塞尔曲线,最后讨论如何由贝塞尔曲线驱动缓动动画并影响动画设计。
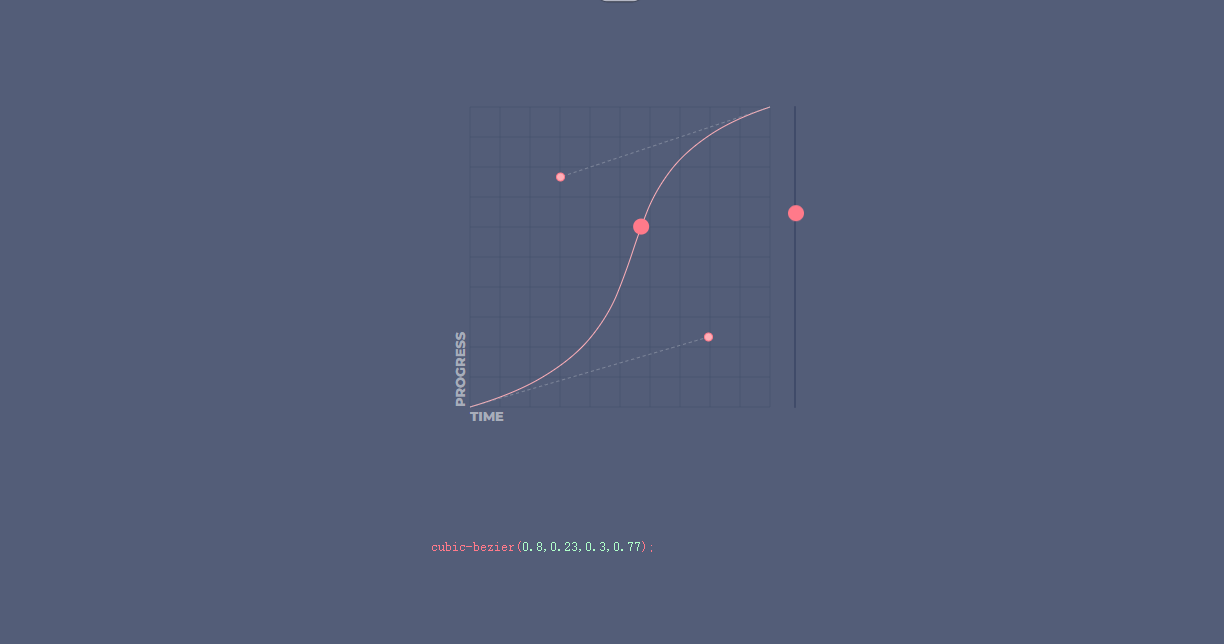
贝塞尔曲线
贝塞尔曲线(Bézier curve)是一种用于绘制平滑曲线的数学工具,由法国工程师皮埃尔·贝塞尔(Pierre Bézier)在20世纪60年代开发,最初用于汽车设计。贝塞尔曲线通过一组控制点来定义,可以通过少量的参数精确地表示复杂的形状。
贝塞尔曲线与动画的关系
贝塞尔曲线在动画制作中有广泛的应用,尤其是在控制动画的运动路径和时间曲线(例如速度曲线)方面。以下是一些常见的应用场景:
- 运动路径:贝塞尔曲线可以用来定义物体在动画中的运动轨迹。例如,在二维或三维动画中,角色或物体可以沿着贝塞尔曲线移动,生成平滑、自然的运动。
- 缓动曲线(Easing Curves):贝塞尔曲线常用于定义动画的缓动效果,决定动画的速度如何随时间变化。常见的缓动效果如“慢入慢出”(Ease In and Ease Out)可以用贝塞尔曲线来实现,这让动画显得更自然和生动。
- 关键帧插值:在关键帧动画中,贝塞尔曲线用于在关键帧之间进行插值,从而生成平滑的过渡动画。通过调整控制点的位置,动画师可以精确控制物体在每个时间点的位置和运动速度。
贝塞尔曲线之所以在动画中如此重要,是因为它提供了一个灵活且直观的方式来控制复杂的动画效果,同时保持高效的计算性能。
运动路径
运动路径是物体在动画中随时间移动的轨迹。通常,这条轨迹可以是直线、圆弧,或更加复杂的曲线。而贝塞尔曲线非常适合描述这些复杂的轨迹,因为它们可以用控制点来灵活地定义曲线的形状。
贝塞尔曲线可以用来生成运动路径的曲线。你可以定义多个控制点,通过这些控制点来控制曲线的形状。物体将沿着这条曲线运动,这样的运动轨迹不仅平滑,还能创造出非常自然的动画效果。
运动路径的步骤
- 定义贝塞尔曲线的控制点
控制点是用来确定贝塞尔曲线形状的关键点。对于一个简单的二次或三次贝塞尔曲线,你至少需要三个或四个控制点。 2. 计算路径上的位置
对于给定的时间 t(通常从 0 到 1),你可以计算贝塞尔曲线上的具体位置 (x, y) 或 (x, y, z)。这个位置就是物体在 t 时间点上的位置。 3. 沿着路径移动物体
在动画过程中,随着时间的推移逐步增加 t 的值,将计算得到的每一个位置应用到物体上,这样物体就会沿着贝塞尔曲线定义的路径运动。
// 定义控制点
const p0 = { x: 50, y: 300 };
const p1 = { x: 150, y: 100 };
const p2 = { x: 250, y: 100 };
const p3 = { x: 350, y: 300 };
/**
* 计算三次贝塞尔曲线插值
* @param {number} t 基于t计算贝塞尔曲线上的点
* @param {Object} p0
* @param {Object} p1
* @param {Object} p2
* @param {Object} p3
* @returns {Object}
*/
function getCubicBezierPoint(t, p0, p1, p2, p3) {
const x = Math.pow(1 - t, 3) * p0.x +
3 * Math.pow(1 - t, 2) * t * p1.x +
3 * (1 - t) * Math.pow(t, 2) * p2.x +
Math.pow(t, 3) * p3.x;
const y = Math.pow(1 - t, 3) * p0.y +
3 * Math.pow(1 - t, 2) * t * p1.y +
3 * (1 - t) * Math.pow(t, 2) * p2.y +
Math.pow(t, 3) * p3.y;
return { x: x, y: y };
}
const result = getCubicBezierPoint(t, p0, p1, p2, p3);
console.log(result);
在三维空间中,贝塞尔曲线可以用于创建更加复杂的轨迹。通过在 x, y, z 维度上使用贝塞尔曲线函数,可以让物体沿着一条三维曲线进行运动。
// 3D 贝塞尔曲线
function cubicBezier3D(t, p0, p1, p2, p3) {
const x = (1 - t) ** 3 * p0.x + 3 * (1 - t) ** 2 * t * p1.x + 3 * (1 - t) * t ** 2 * p2.x + t ** 3 * p3.x;
const y = (1 - t) ** 3 * p0.y + 3 * (1 - t) ** 2 * t * p1.y + 3 * (1 - t) * t ** 2 * p2.y + t ** 3 * p3.y;
const z = (1 - t) ** 3 * p0.z + 3 * (1 - t) ** 2 * t * p1.z + 3 * (1 - t) * t ** 2 * p2.z + t ** 3 * p3.z;
return { x, y, z };
}
// 示例代码与二维类似,区别是考虑了 `z` 维度,需要使用了 3D 绘图工具来显示结果。
缓动曲线
缓动曲线(Easing Curve)是用来控制动画在时间轴上的速度变化的一种曲线。它决定了动画从一个状态过渡到另一个状态的速度方式,例如慢慢加速、逐渐减速等。缓动曲线通常通过一个函数来实现,该函数接受一个时间参数(通常归一化到0到1的范围),返回一个表示进度的值。
而常见的缓动函数有:
线性(Linear):
直线,表示匀速运动。
- 动画匀速进行。
- 函数:f(t) = t
// 线性缓动
function linear(t) {
return t;
}
缓入(Ease In):
曲线从平缓到陡峭,表示加速运动。
- 动画开始时较慢,然后加速。
- 常见函数:f(t) = t^n(通常 n = 2 或 3)
// 缓入(Ease In)
function easeInQuad(t) {
return t * t;
}
缓出(Ease Out):
曲线从陡峭到平缓,表示减速运动。
- 动画开始时较快,然后减速。
- 常见函数:f(t) = 1 - (1 - t)^n(通常 n = 2 或 3)
// 缓出(Ease Out)
function easeOutQuad(t) {
return t * (2 - t);
}
缓入缓出(Ease In Out):
曲线从平缓到陡峭再到平缓,表示先加速后减速的运动。
- 动画开始时较慢,中间加速,然后在结束时减速。
- 常见函数:f(t) = 0.5 * (1 - cos(π * t))
// 缓入缓出(Ease In Out)
function easeInOutQuad(t) {
return t < 0.5 ? 2 * t * t : -1 + (4 - 2 * t) * t;
}
通过这些缓动函数,可以让动画看起来更加自然和流畅,不再是简单的匀速运动。
贝塞尔缓动曲线
贝塞尔缓动曲线允许你通过控制点的配置,创造出各种非线性运动效果,比如缓入、缓出、以及缓入缓出等。
贝塞尔曲线可以用作缓动曲线的一种方式,因为它可以通过控制点精确地控制动画的加速度和减速度。我们常用的贝塞尔缓动曲线是三次贝塞尔曲线,它有两个控制点,起始点 (0, 0) 和终点 (1, 1) 是固定的。
三次贝塞尔曲线公式
三次贝塞尔曲线的公式如下:
其中,P0 是起点 (0, 0),P3 是终点 (1, 1),P1 和 P2 是两个控制点。
使用贝塞尔曲线实现缓动 假设我们有两个控制点 (cx1, cy1) 和 (cx2, cy2),我们可以用这四个点来定义一个三次贝塞尔曲线,作为缓动函数。
参数解释
cx1, cy1, cx2, cy2:是两个控制点的位置,cx1 和 cy1 控制曲线在 t 近 0 的部分的形状,cx2 和 cy2 控制曲线在 t 近 1 的部分的形状。 t:表示当前时间,范围在 0 到 1 之间。
代码实现
贝塞尔曲线通常定义在二维空间中,包括 x 和 y 两个维度。在动画缓动的上下文中:
- x 轴 通常表示时间进度(从 0 到 1)。
- y 轴 表示动画属性的变化(例如位置、透明度等)。
因此我们很容易忽略x轴,直接取y作为缓动的结果使用,并写出这样的实现:
// 三次贝塞尔曲线的缓动函数
function cubicBezierEase(t, cx1, cy1, cx2, cy2) {
// const x = cubicBezier(t, 0, cx1, cx2, 1);
const y = cubicBezier(t, 0, cy1, cy2, 1);
// 由于 x 是时间,返回 y 作为缓动曲线的结果
return y;
}
// 计算贝塞尔曲线上的一点
function cubicBezier(t, p0, p1, p2, p3) {
const u = 1 - t;
return Math.pow(u, 3) * p0 +
3 * Math.pow(u, 2) * t * p1 +
3 * u * Math.pow(t, 2) * p2 +
Math.pow(t, 3) * p3;
}
// 示例使用,基于 CSS 的缓动曲线
const cx1 = 0.42, cy1 = 0, cx2 = 0.58, cy2 = 1;
const result = cubicBezierEase(0.5, cx1, cy1, cx2, cy2);
console.log(result);
然而,在前面的实现中,我们直接使用贝塞尔曲线的 y 轴值来表示缓动结果,而没有考虑 x 轴的实际非线性关系。这导致了输出动画并不正确,与 CSS 的 cubic-bezier() 不一致。
被忽略的X
在贝塞尔曲线中,时间 t 是一个参数化变量,定义了曲线上每个点的位置。标准的贝塞尔曲线公式中,x 和 y 都是 t 的函数,即:
其中 B_x(t) 和 B_y(t) 是分别描述 x 和 y 坐标的贝塞尔曲线函数。
当 x 代表时间进度时,我们通常知道时间 t,并且希望找出对应的 y 值来控制动画效果。然而,贝塞尔曲线的 x 和 y 坐标是互相独立的函数,并不是线性的。所以给定时间 t 对应的 x 值,我们需要计算出对应的 y 值,这就是“反解”过程。
因此在实现中,x 轴表示时间进度,需要对时间 t 进行反解,以确保动画进度按预期沿 x 轴移动。这通常是通过数值解法(如牛顿法)来求解的。
为了使结果与 CSS 中的 cubic-bezier() 一致,我们需要在计算缓动结果时,先找到时间 t 对应的 x 值,然后用这个 x 值求得正确的 y 值。
function cubicBezierEase(t, cx1, cy1, cx2, cy2) {
// 通过数值求解方法来找到给定 t 对应的 x 值
const x = solveCubic(t, cx1, cx2);
const y = cubicBezier(x, 0, cy1, cy2, 1); // 使用 x 计算 y
return y;
}
function solveCubic(t, cx1, cx2, epsilon = 1e-5) {
let x = t, prevX;
do {
prevX = x;
x = x - (cubicBezier(x, 0, cx1, cx2, 1) - t) / derivativeBezier(x, cx1, cx2);
} while (Math.abs(x - prevX) > epsilon);
return x;
}
function derivativeBezier(t, p1, p2) {
const u = 1 - t;
return 3 * u * u * (p1) + 6 * u * t * (p2 - p1) + 3 * t * t * (1 - p2);
}
function cubicBezier(t, p0, p1, p2, p3) {
const u = 1 - t;
return Math.pow(u, 3) * p0 +
3 * Math.pow(u, 2) * t * p1 +
3 * u * Math.pow(t, 2) * p2 +
Math.pow(t, 3) * p3;
}
// 示例使用,基于 CSS 的缓动曲线
const cx1 = 0.42, cy1 = 0, cx2 = 0.58, cy2 = 1;
const result = cubicBezierEase(0.5, cx1, cy1, cx2, cy2);
console.log(result);
贝塞尔曲线参数示例
- Ease In (缓入):
cubicBezierEase(t, 0.42, 0, 1, 1) - Ease Out (缓出):
cubicBezierEase(t, 0, 0, 0.58, 1) - Ease In Out (缓入缓出):
cubicBezierEase(t, 0.42, 0, 0.58, 1)
说明
当 cy1 和 cy2 接近 0 或 1 时,会导致缓动曲线更接近于直线(即线性缓动)。 不同的控制点组合可以产生非常多样化的缓动效果。
通过这种方式,动画师可以精确控制动画的缓动效果,使其更符合现实中的运动效果。
